Векторы и матрицы
Реляционные базы данных разрабатываются в расчете на масштабирование при росте объема данных. Здесь описывается, как мы представляем крупные "векторные" и "матричные" объекты в виде отношений и реализуем над ними логические операции. Это дает нам векторную арифметику.
До построение операций нам нужно определить, что означает "вектор" (часто в форме матрицы) в контексте базы данных. Имеется много способов разделения таких матриц ("блоками", "порциями" ("chunk")) по узлам параллельной системы (см., например, , гл. 4). Простой способ, хорошо подходящий для параллельных баз данных, состоит в представлении матрицы в виде отношения со схемой (row number integer, vector numeric[]) и разрешении СУБД разделять строки между процессорами произвольным образом – например, на основе хэширования или циклической схемы. На практике мы часто материализуем и A, и A´, чтобы этот метод построчного представления работал более эффективно.
Для матриц, представляемых подобным образом в виде горизонтально разделенных отношений, нам нужно реализовать базовую матричную арифметику в виде запросов над этими отношениями, чтобы эти запросы могли выполняться параллельно.
Рассмотрим две матрицы A и B одной и той же размерности. На SQL легко выражается сложение матриц:
SELECT A.row_number, A.vector + B.vector FROM A, B WHERE A.row_number = B.row_number;
Заметим, что здесь операция "+" выполняется над массивами числовых типов и возвращает массив той же размерности, так что на выходе получается матрица той же размерености, что и у матриц-операндов. Если в СУБД не поддерживается операция сложения векторов, ее легко реализовать с использованием объектно-реляционных расширений и зарегистрировать как инфиксную операцию . Для выполнения этого запроса оптимизатор запросов, вероятно, выберет метод соединения с хэшированием, который хорошо распараллеливается.
Умножение матрицы на вектор Av также выражается просто:
SELECT 1, array_accum(row_number, vector*v) FROM A;
Здесь снова операция "*" выполняется над массивами числовых значений, но в этом случае она возвращает одно числовое значение – скалярное произведение операндов:
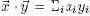
В большинстве РСУБД имеются функции над последовательностями. В PostgreSQL и Greenplum команда generate series(1, 50) сгенерирует последовательность 1, 2, ..., 50. Один из способов вычисления транспонированной матрицы A´ для матрицы A размерности m×n можно выразить на SQL следующим образом (для n = 3):
SELECT S.col_number, array_accum(A.row_number, A.vector[S.col_number]) FROM A, generate_series(1,3) AS S(col_number) GROUP BY S.col_number;
К сожалению, если A хранит n-мерные вектора, то в операции группирования будут участвовать n копий таблицы A. Альтернативой является переход к другому представлению матриц, например, к разреженному представлеению вида (row number, column number, value). Преимущество такого подхода состоит в том, что в этом случае на SQL гораздо легче выразить операцию перемножения матриц AB:
SELECT A.row_number, B.column_number, SUM(A.value * B.value) FROM A, B WHERE A.column_number = B.row_number GROUP BY A.row_number, B.column_number
Этот запрос очень эффективно выполняется над разреженными матрицами, если в них не сохраняются нулевые значения. Вообще говоря, хорошо известно, что никакое одно представление не удовлетворяет все потребности, и на практике приходится использовать смеси. При отсутствии должной абстракции это может привести к путанице, посколько для каждого представления нужно определять специальные операции.
В SQL разные представления можно получить за счет соглашений об именовании (материализованных) производных таблиц, но выбор такой таблицы обычно производится аналитиком, поскольку традиционный оптимизатор запросов не знает об эквивалентности этих производных таблиц. Результаты исследования в этом направлении описаны в литературе по параллельным вычислениям , но их еще требуется интегрировать с механизмами оптимизации запросов и поддержки вычислений над данными большого объема.
Приведенные рассуждения применимы к операциям скалярного умножения, сложения векторов и умножения векторов/матриц, которые по своей сути являются однопроходными методами. Задача деления матриц в параллельно контексте не решена окончательным образом. Одно из неудобств SQL состоит в отсутствии удобного синтаксиса для организации итераций. Фундаментальные методы вычисления обратной матрицы предполагают два или большее число проходов по данным. Однако рекурсивные или итеративные процедуры могут выполняться во внешних процессах с минимальным объемом потока данных с основного узла. Например, в методе сопряженных градиентов, описываемом в п. 5.2.2, между итерациями запрашивается всего одно значение. Хотя деление матриц усложнено, мы можем разработать оставшуюся часть методов, описываемых в этой статье, на основе процедур псевдоинверсии (с учетом предупреждений, приводимых в учебниках по математики по поводу существования и сходимости).
Обширный набор (теперь распределенных) векторных объектов и операций над ними образует существительные и глаголы математических статистиков. В этом смысле функции действуют как высказывания. Мы продолжим рассмотрением знакомого примера, выраженного на этом языке.
